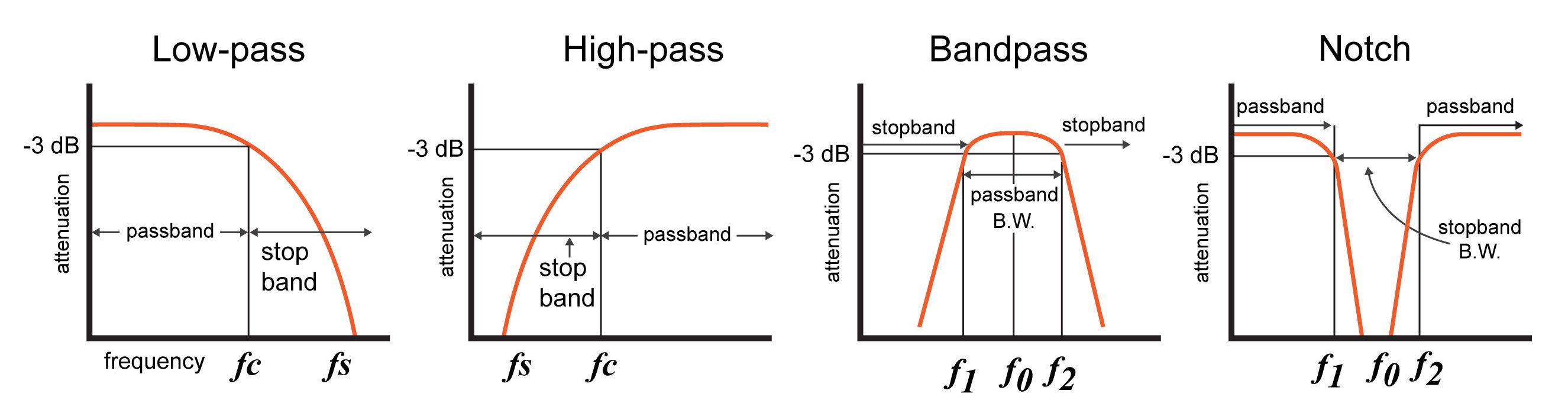
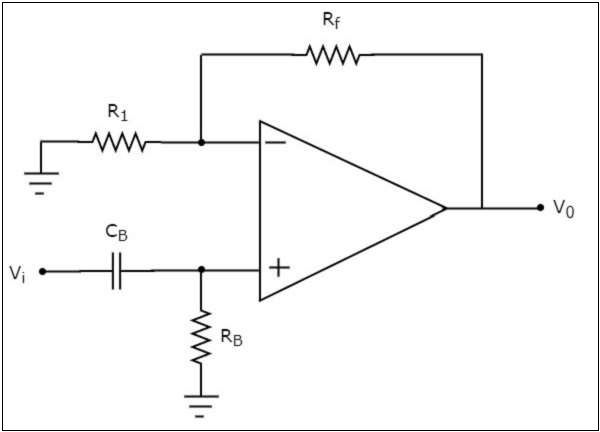
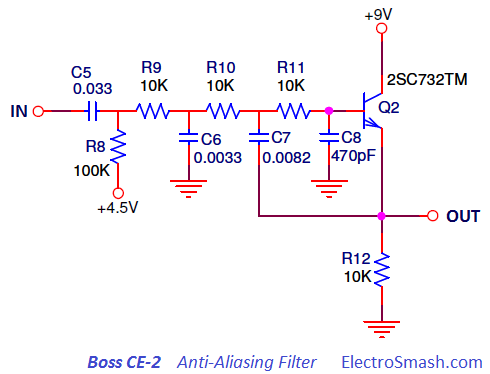
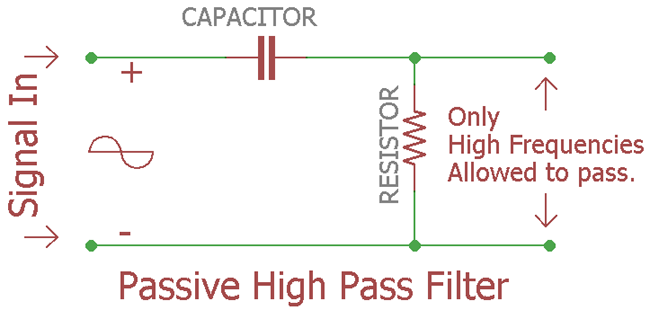
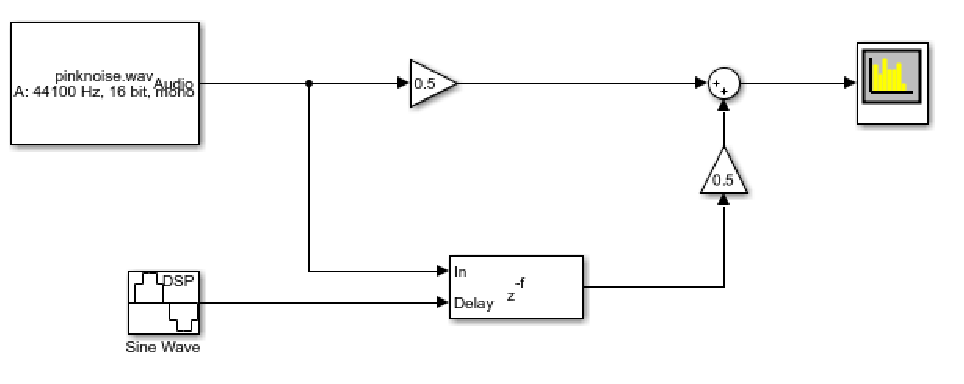
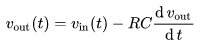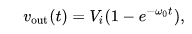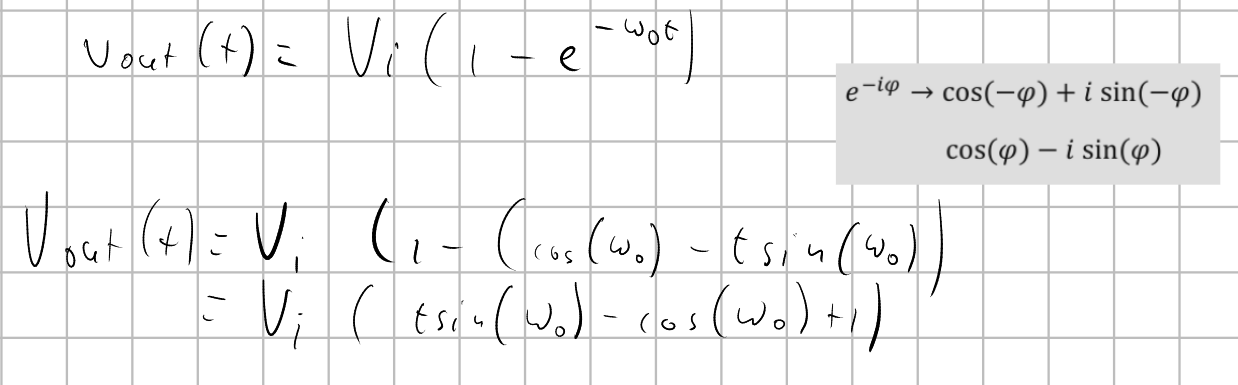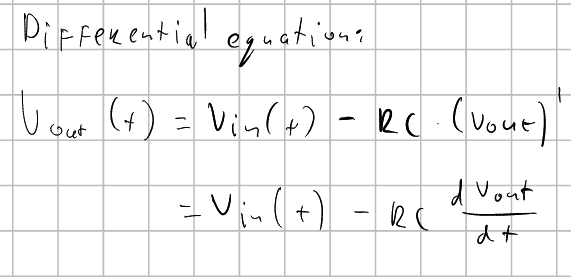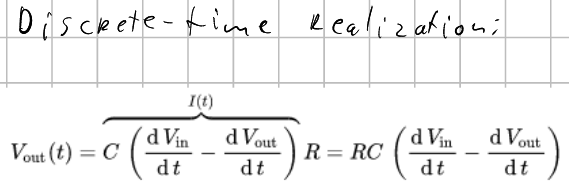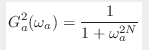Low-Pass filter
(from wikipedia) A low-pass filter is a filter that passes signals with a frequency lower than a a selected cutoff frequency. Some low-pass filters also attenuate signals with frequencies higher than the cutoff frequency.
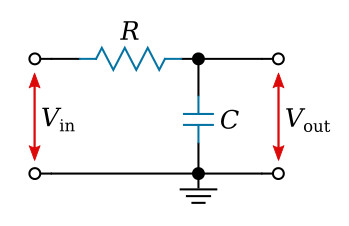
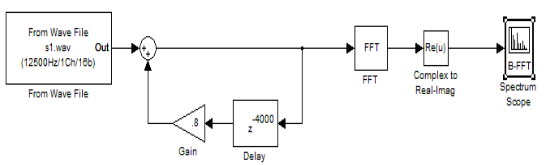
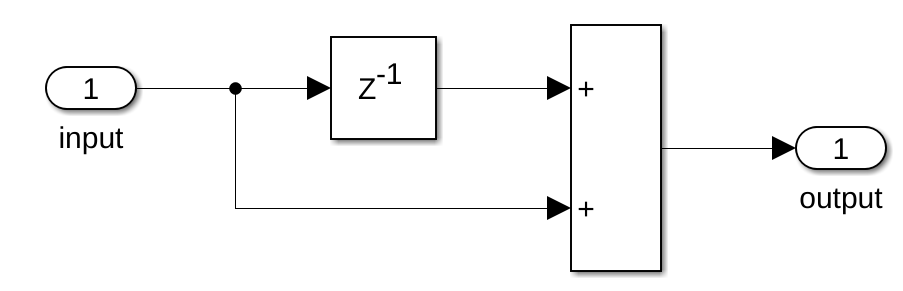
As stated in this simplest lowpass filter article, the most simple lowpass filter has the form y[n] = x[n] + x[n-1]. It's model looks like this:
The differential equation of a low-pass filter can be described as:
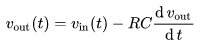
The step input response has the solution:
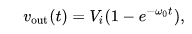
In this function, w0 = 1/RC is the cutoff frequency of the filter.
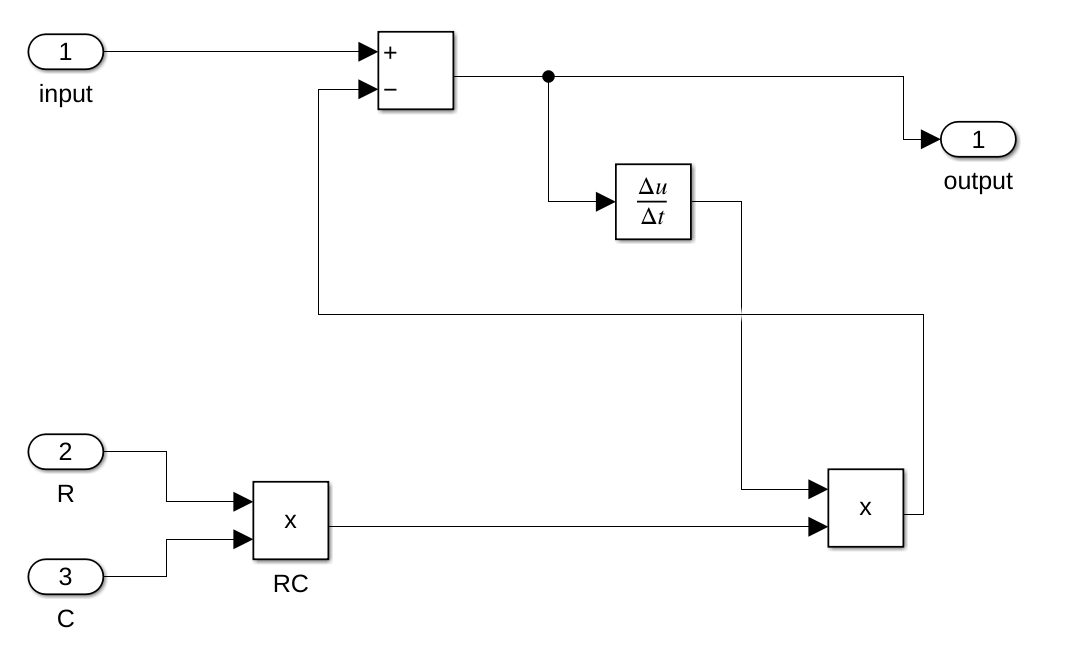
If we put the differential equation into Simulink, we get the following model:
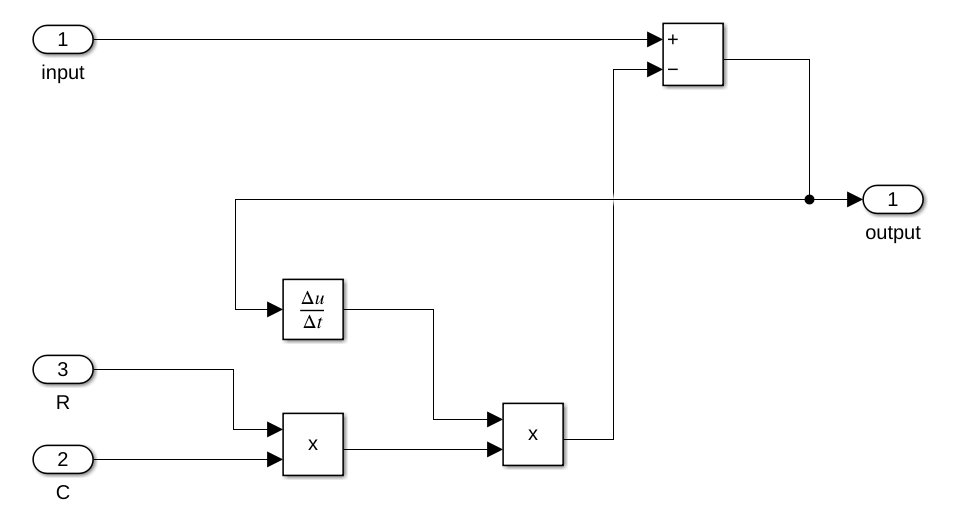
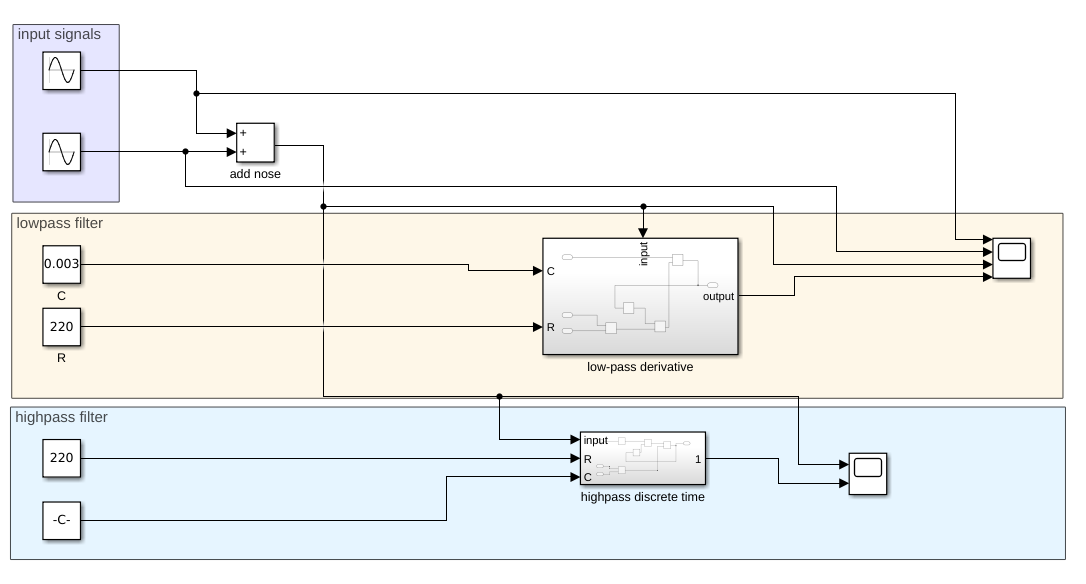
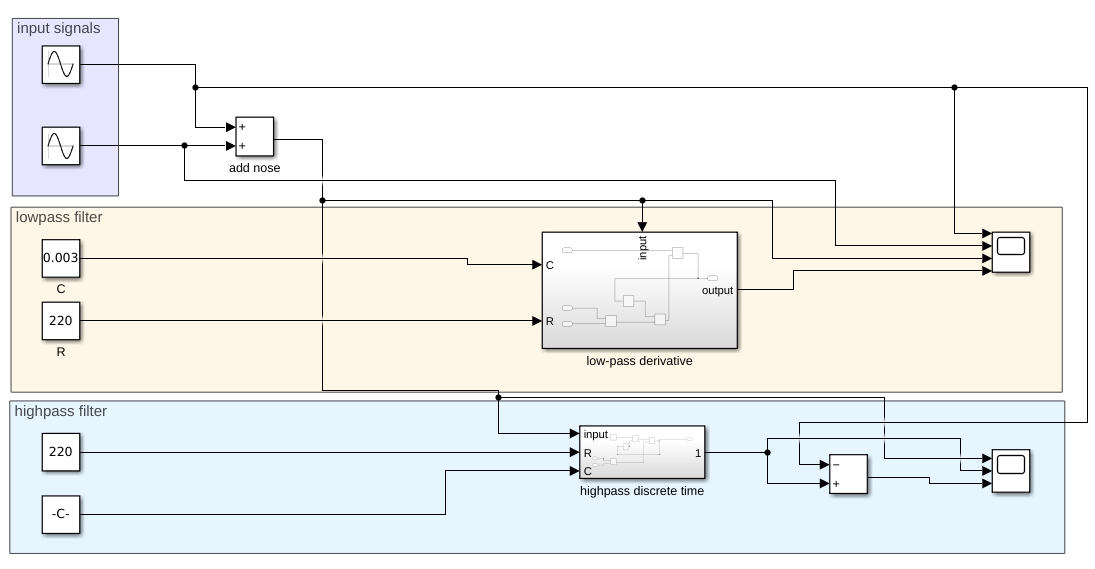
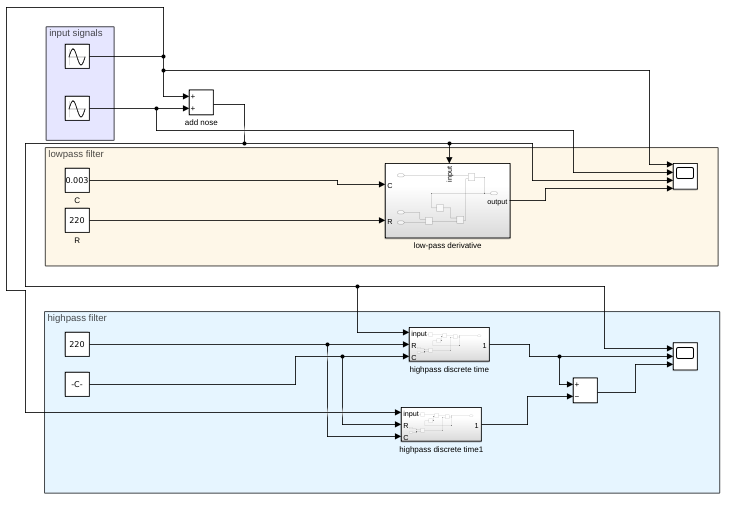
Putting this subsystem into a model with input signals, the following model can be made:
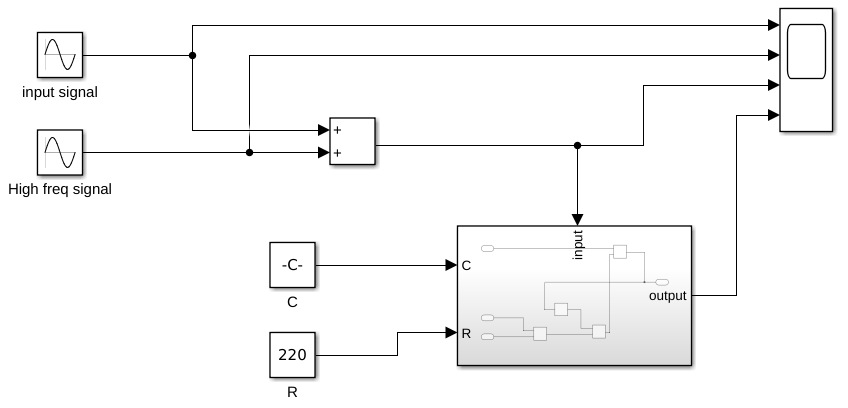
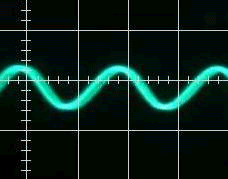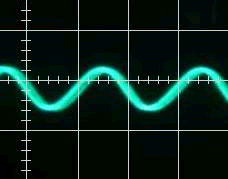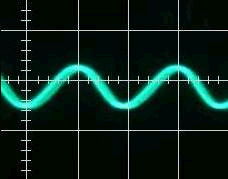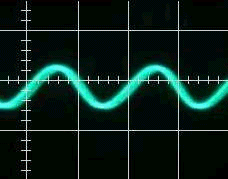
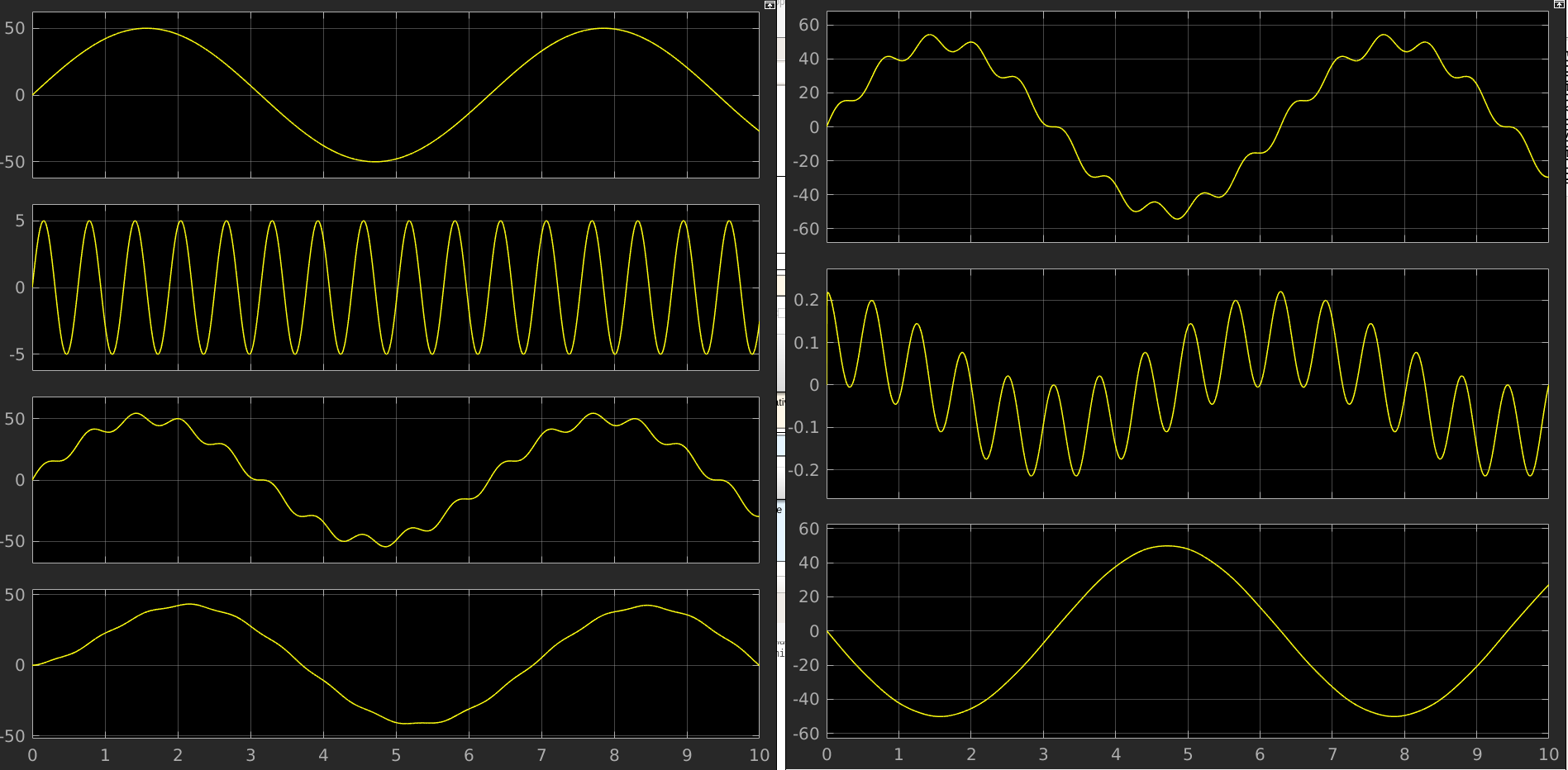
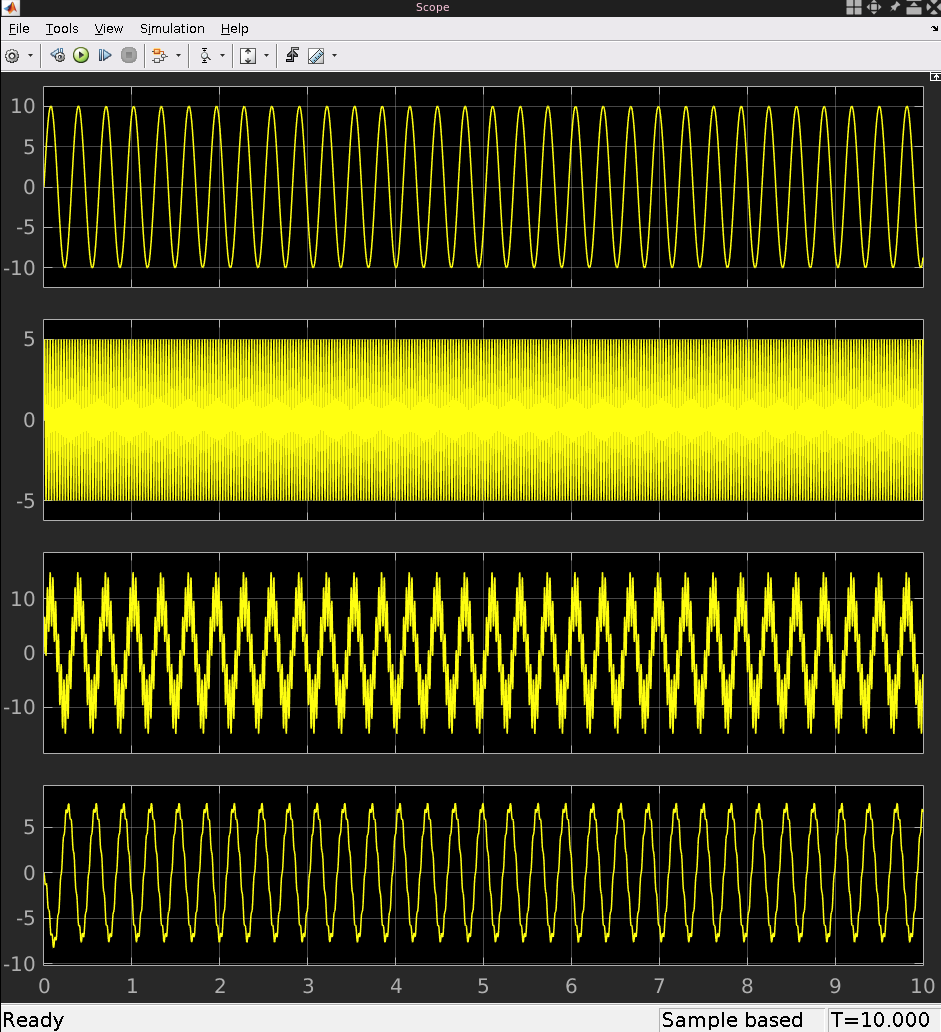
Here I have chosen a value of 220 Ohm for R and 300uF for C. The input signal has a frequency of 10 Hz with an amplitude of 10. The high frequency signal functions as noise and has a frequency of 10x the input frequency and half the amplitude of the input frequency. The result is as follows:
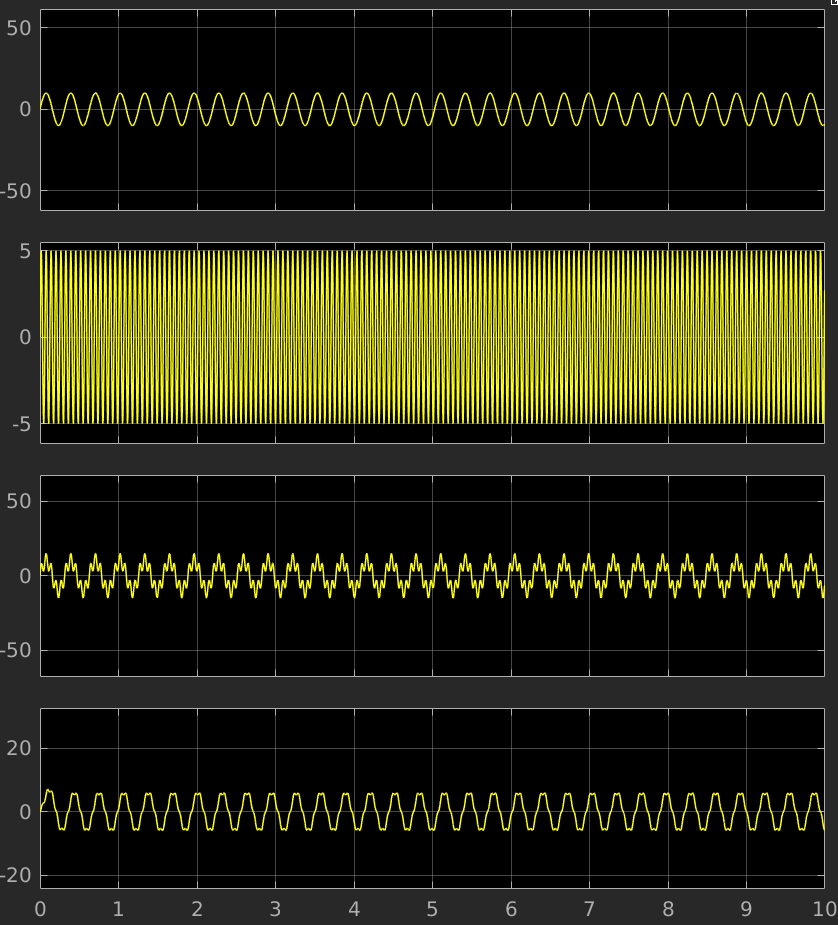
You can see that the low-pass filter works by filtering out the high frequency noise in the input signal. It is not perfect, as the output signal does not 100% represent the input signal, but it serves as a demonstration purpose
The step impulse equation can be rewritten using equation 1.18 on page 17 from Paul A. Lynn's book to the form:
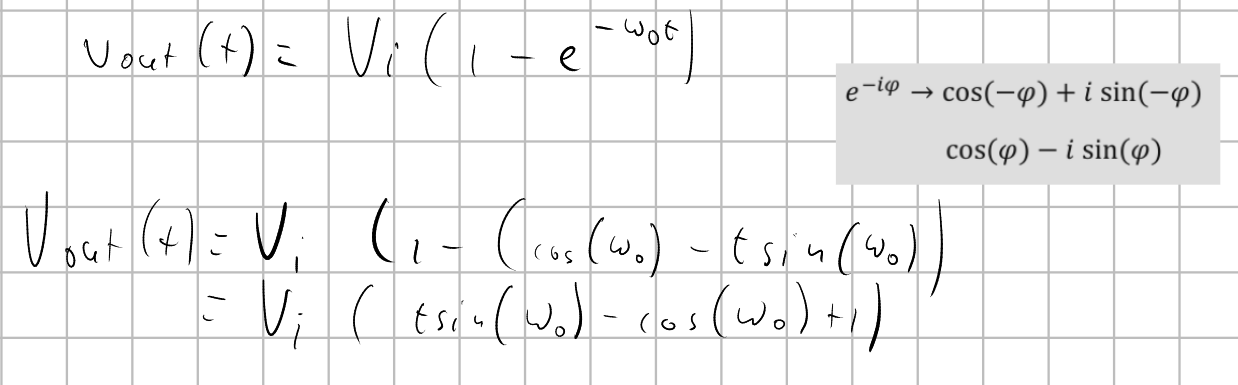
If we again look at the wikipedia article for low-pass filters, we can look at the difference equation through discrete time sampling. If we use that formula and use the fact that we are working with DSP signals and can omit the T variable (as said in the article about the simplest low-pass filter), we can get a new equation for the low-pass filter:

In this equation, the w0 is the cutoff frequency, described by 1/RC. The next problem to solve is figuring out how we can set the value of a gain block in Simulink to exp(1/RC). There is some useful information about the gain block itself here, but it doesn't tell us how we can use an input for a gain block to set its value. This video contains some information about base and model workspaces. In the MATLAB workspace, I made two values for R and C, and defined a variable w0 = 1/(R*C). For testing, I set the value for R to 220 Ohm and C to 4.7 uF. However, when I wanted to set the gain value to the w0 variable, I got this error:
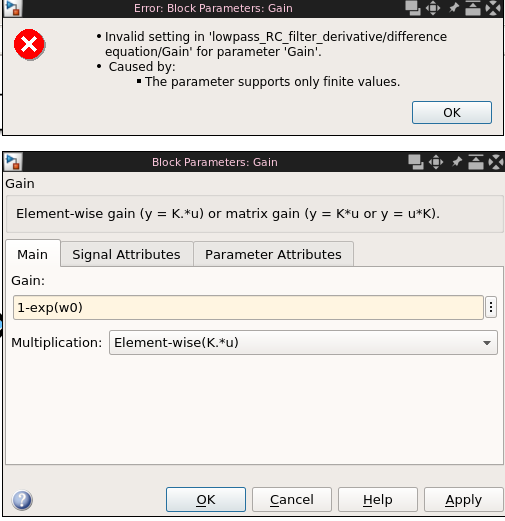
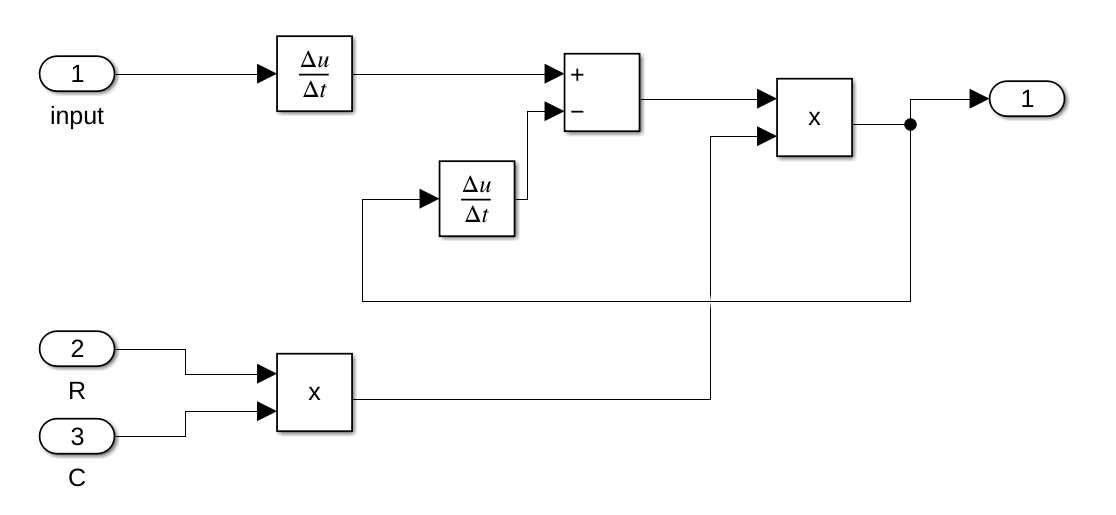
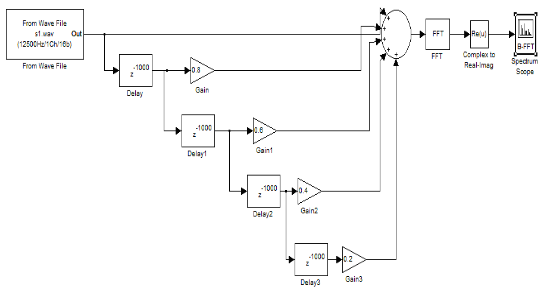
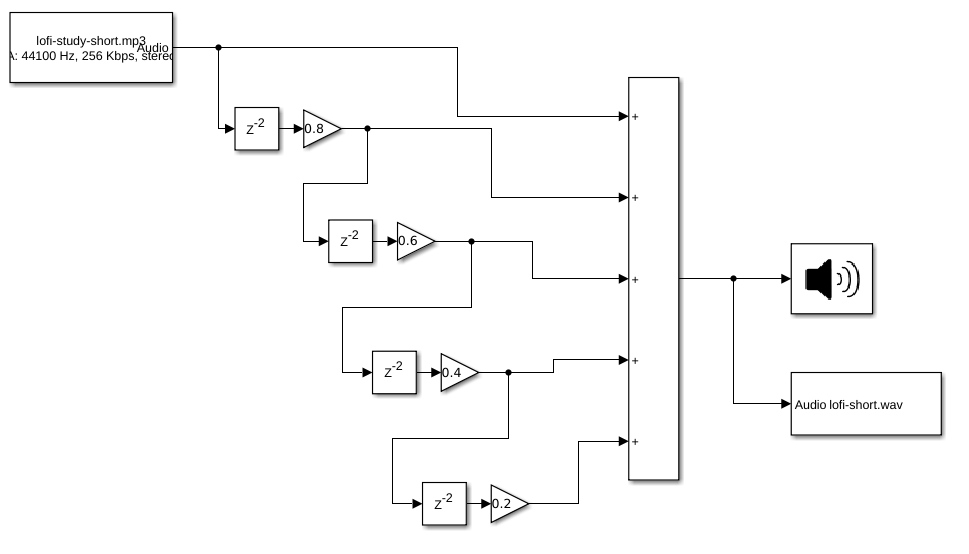
The problem was that the value of w0 was way too big. It was 1/(220 * 4.7-6), which is 967.1180. Because of this, the value for e-w0 was basically 0. To fix this, I changed C to 0.022, which changed w0 to 0.2066. After that, setting the gain value worked. I implemented the difference equation in a simulink model:
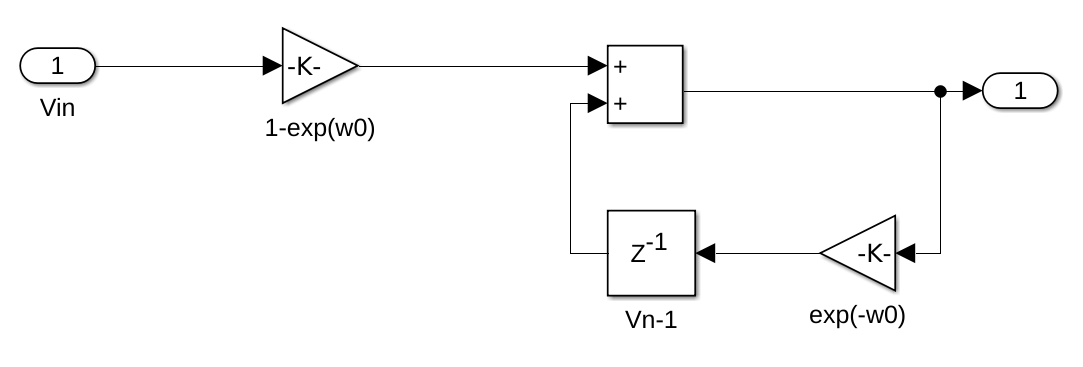
Using this subsystem, I added this into the model:
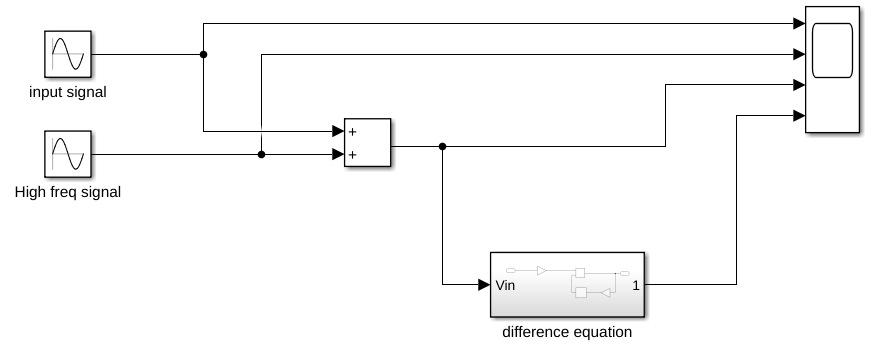
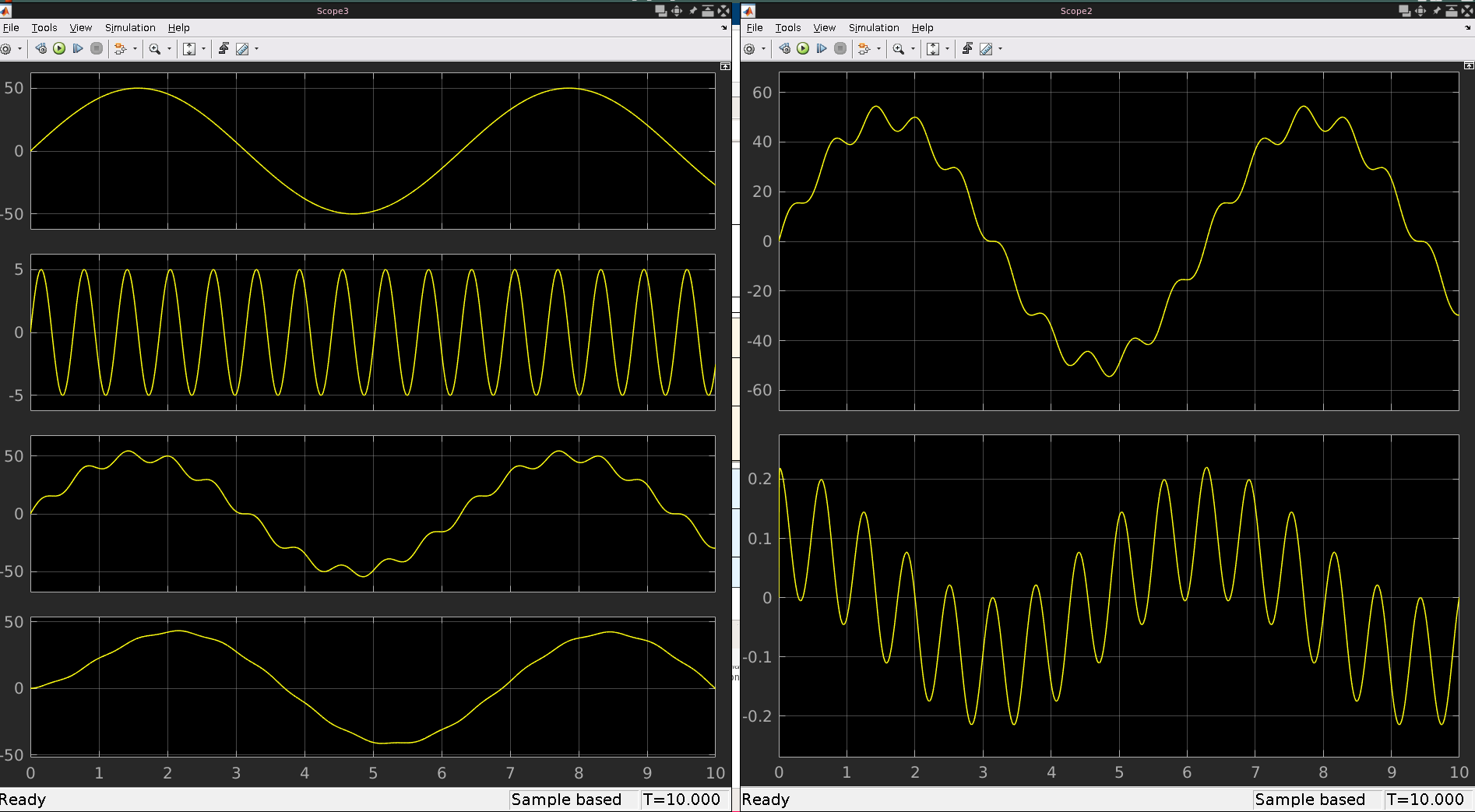
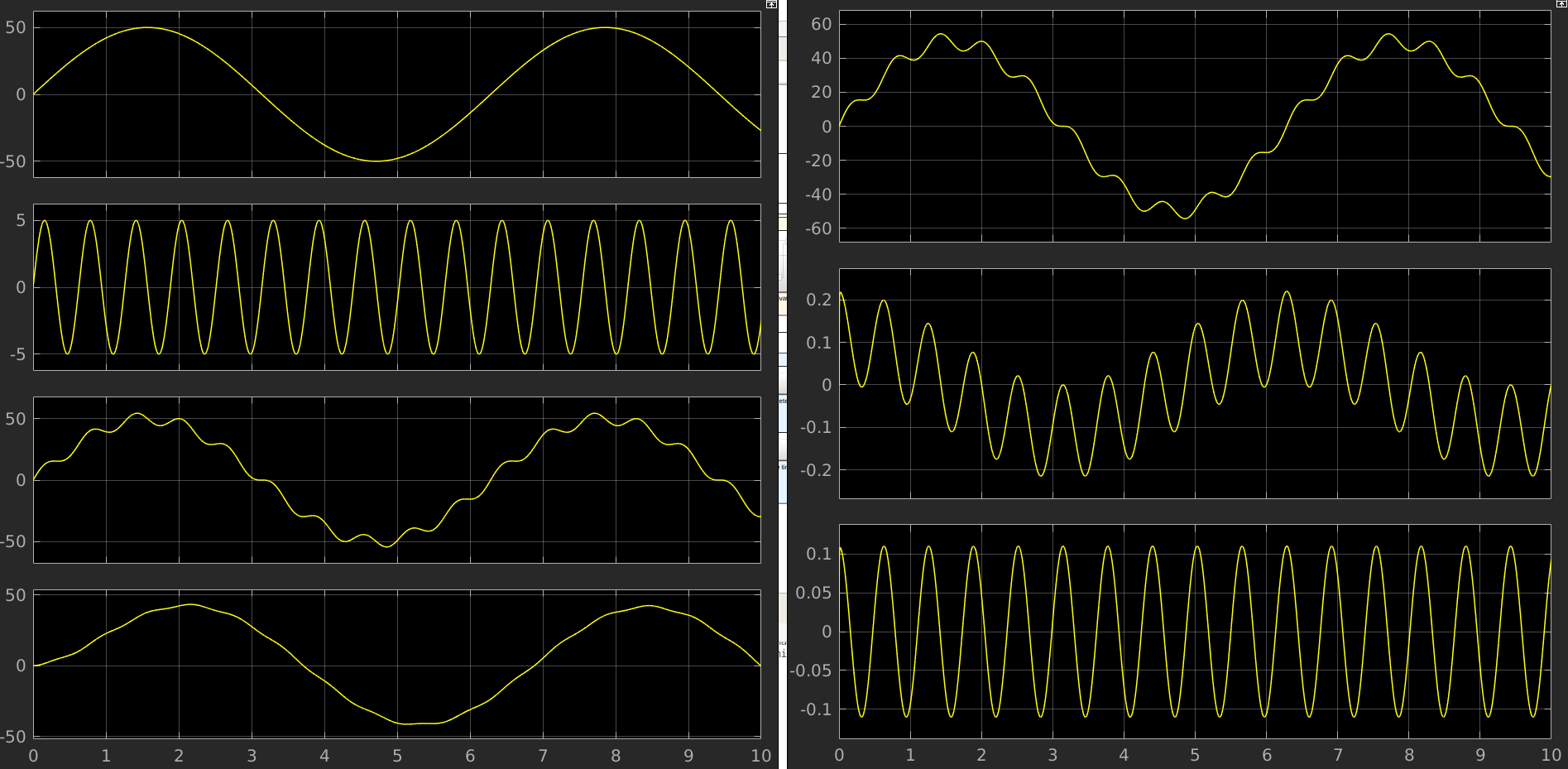
After that, I ran the model, and got the following result:
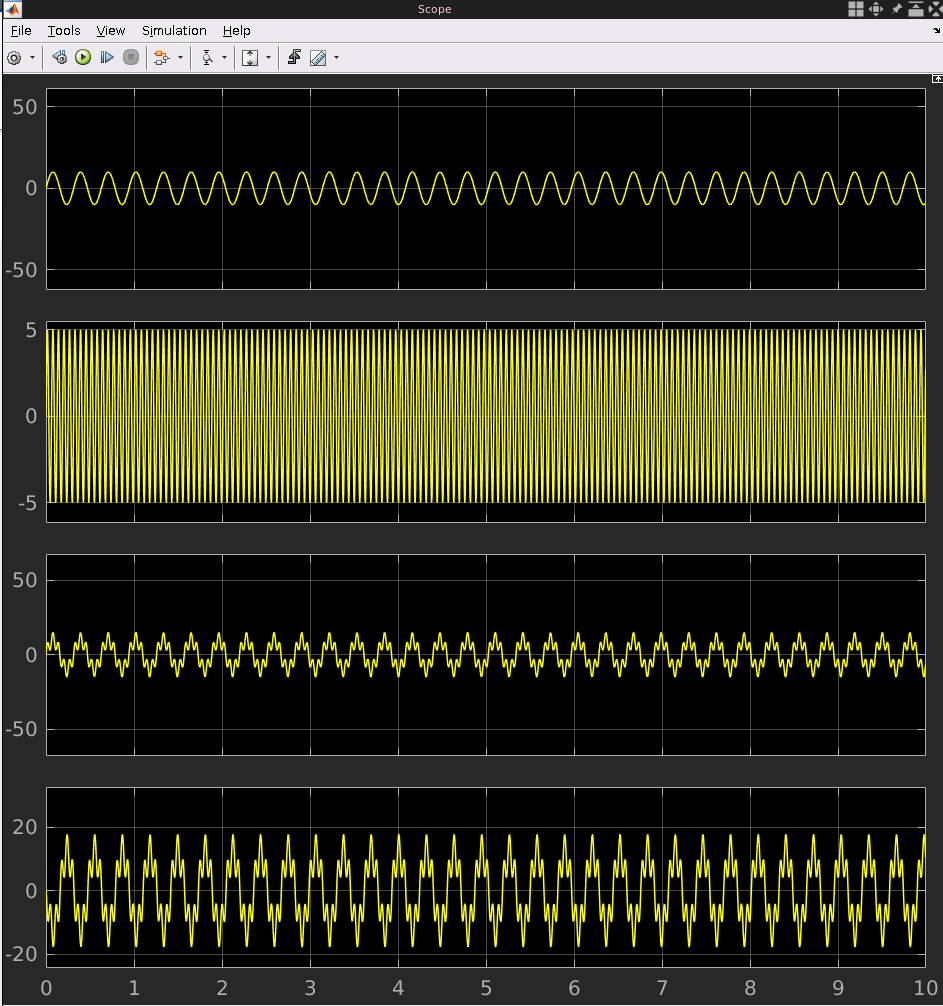
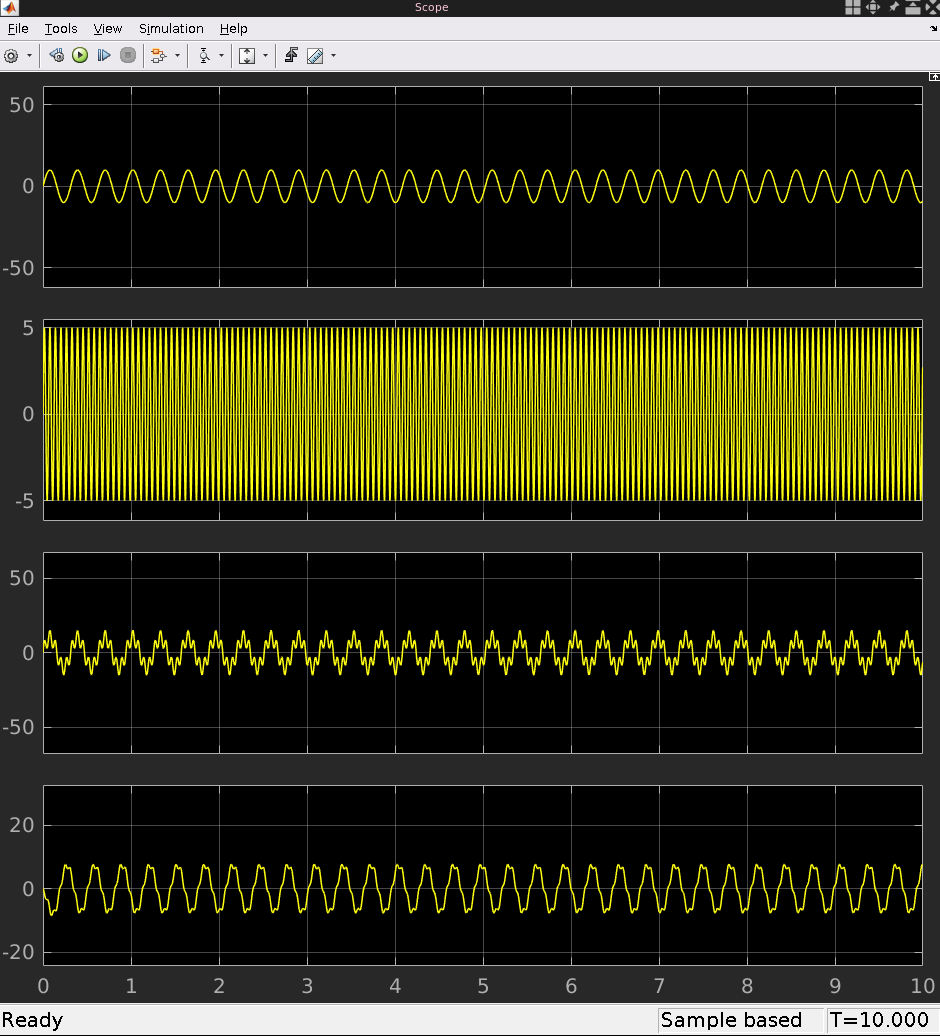
As you can see, the filter does not really work as expected, It seems to enhance the high frequencies instead of lower them. The problem is that the value of w0 is too high. If it's too close to 1, the filter won't do anything. So, I changed the value of w0 to 0.02066 to see how that affected the result. As you can see, this result is more promising. I also readjusted the y-axis of the scope to better see the signal.
The Simulink file for the models can be found here in the library